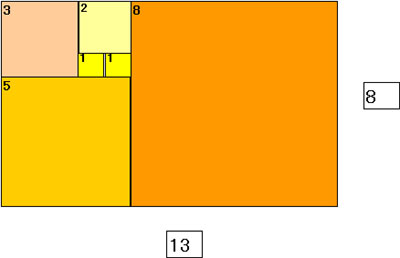
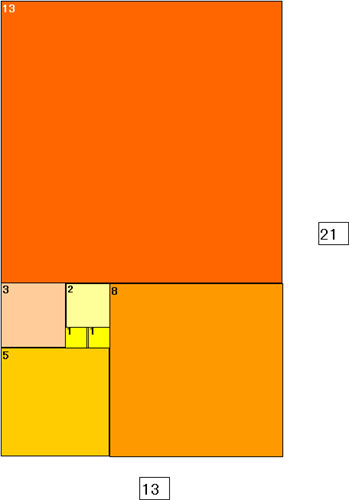
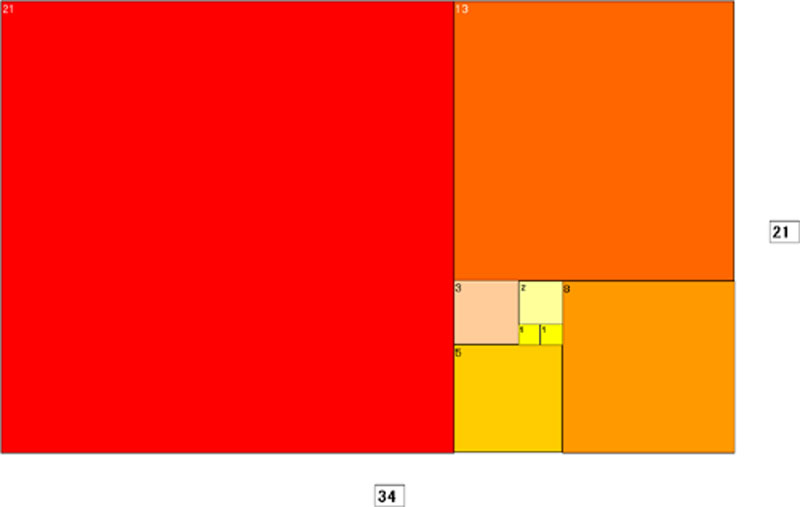
ここでは、フィボナッチ数列を勉強します。
| つぎのような数列があります。空白にはどんな数が入るでしょうか。
一見しただけで、すぐに答えがわかった人もいるかと思います。 「ダ・ヴィンチ・コード」(ダン・ブラウン著)のなかでは、「13-3-2-21-1-1-8-5
O,Draconian devil! Oh,lame saint
しばらくじっとこの数列を観察していますと、第3項、第4項、第5項はそれぞれ、 第3項=第1項+第2項 すなわち 2=1+1 第4項=第2項+第3項 すなわち 3=1+2 第5項=第3項+第4項 すなわち 5=2+3 のように一定の規則にしたがってできていることに気がつくとおもいます。 この数列の各項は連続する直前の2つの項の和になっているわけです。 こたえは、「8」と「21」ということになります。
小説の「ダ・ヴィンチ・コード」ではこの暗号 「13-3-2-21-1-1-8-5 O,Draconian devil !! Oh,lame saint(おお、ドラコンのごとき悪魔め!)(おお、役立たぬ聖人め!)」 に対し、次のように並べ替え、解読した。 →1-1-2-3-5-8-13-21に沿って、この2行を並べ替えると・・ Leonard da Vince!! The Mona Lisa! 「モナリザ」
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
このような性質をもった数列は、今からおよそ800年前の1202年に数学者レオナルド・フィボナッチが著した、"Liber Abacci"すなわち『算盤の書』の中ではじめて見られます。
イタリアの数学者レオナルド・デ・ピサ(Leonardo
de Pisa)は1175年頃にピサで生まれました。彼はフィボナッチ(Fibonacci)という名前で広く知られていますが、これはボナッチオの息子(Filius
of Bonaccio)を短縮したものです。彼の父ボナッチオ(Bonaccio)は、アフリカ北海岸の都市ブジア(Bugia)、現在のアルジェリアのブジーの関税官でした。そのためフィボナッチは、バーバリ(Barbary)のイスラム人による教育を受け、アラビア式の数体系を学びました。1200年頃にピサに戻って、
多数の数学論文を書いています。 『算盤の書』には、以下に述べる1つがいの兎の子孫についても問題を提起しています。
この問題の毎月のうさぎのつがいの数がフィボナッチ数列になるというわけです。 図で一番小さいのが生まれたばかりの1つがいのうさぎ。2番目に小さな(中間の)うさぎは生まれて1ヵ月のうさぎ。 規則にしたがってうさぎが増え続けるときの6カ月後までのうさぎの増え方を示しています。
この図をもとにうさぎの増え方を観察し、どの月でも共通なアルゴリズムを見出すことができるでしょうか。 最下段の6ヶ月後のつがいの数に注目して考察してみましょう。 6ヵ月には 6ヵ月後のうさぎのつがいの数は、前々月の4ヵ月後にいる(親と子を合わせた)つがいの数に、 これを7ヵ月以降にも適用していくと、
つがいの数は233ということになります。
この数列はフィボナッチ数列と呼ばれています。 現在も、【フィボナッチ協会】があり、下記のような正式な定義を決めています。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
フィボナッチ数列の生成規則は,ウサギのつがいの増加や細胞の増加の様子をうまく模倣しているように,自然界に潜むある規則を表しているように見えます。また黄金比の性質は,美しいだけでなく,長方形の中にぴったり収まるという意味で形の上での最適な状況を表しています。これらが自然界の様々なものの中に頻繁に見つけることができます。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
定義にしたがってフィボナッチ数を実際に求め、最初の45個F1〜F45をリストアップすると下の表になります。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
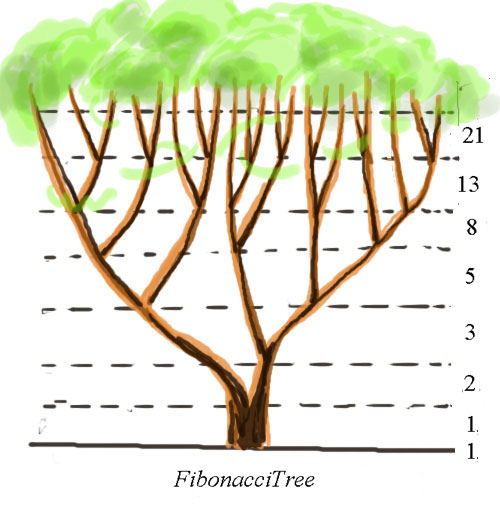
木の枝の分岐は、太陽をもとめて回転しながら、順次上にのびていきます。 1,2,4,8というような倍々のふえかたではなく、1,2,2,3,5,8,13というようにすこし控えめな増え方が自然界ではおおいようです。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
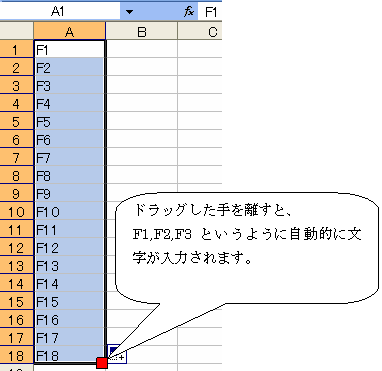
この数にはさまざまな性質があります。ひとつExcelで実験してみましょう。 Excelシートを表示させてください。セル[A1]にまず「F1」というフィボナッチ数列の番号を入力します。
セル[A1]のオートフィルボタン(セル[A1]を選択し、右下隅にマウスを置くとマウスの先が、+マークに変化します)をセル[A46]あたりまでドラッグしてください。
F1〜F46などと、表示されます。
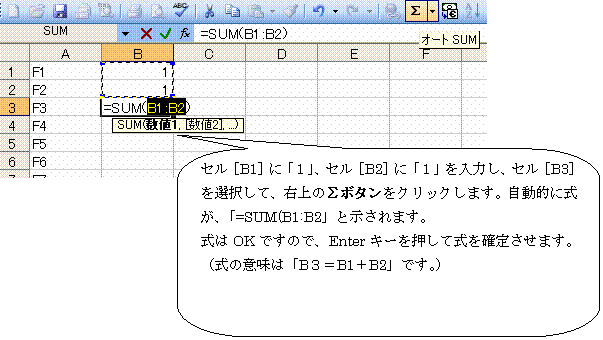
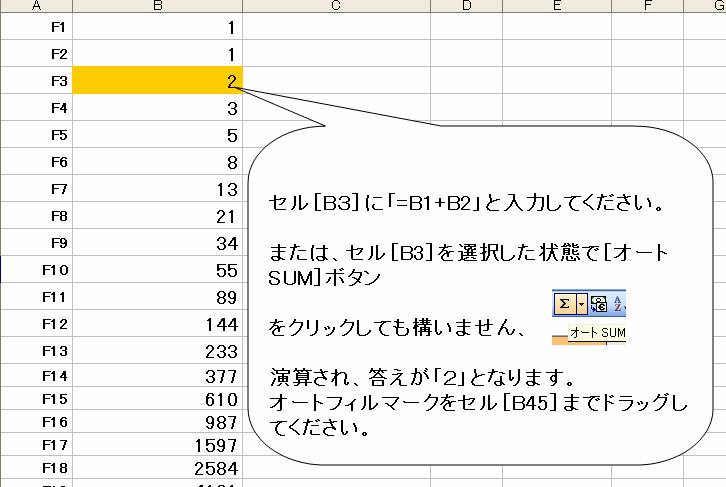
セル[B1]にF1(フィボナッチ数列F1)である「1」を入力してください。
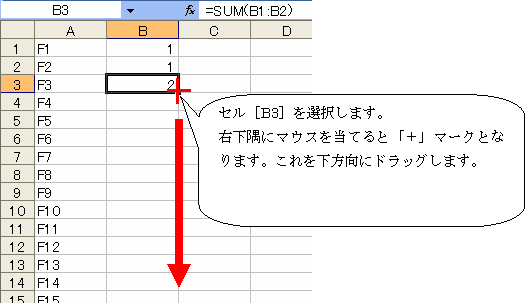
セル[B3]のオートフィルボタンをつかみ、セル[B46]までドラッッグしてください。
表示される数値がフィボナッチの数列となります。ちなみにセル[B46]=1,836,311,903となっているはずです。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
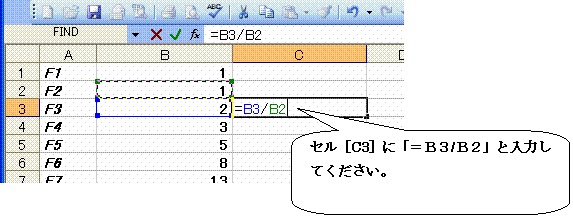
性質その1・・・ 隣り合う2つのフィボナッチ数の比を求めてください。
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
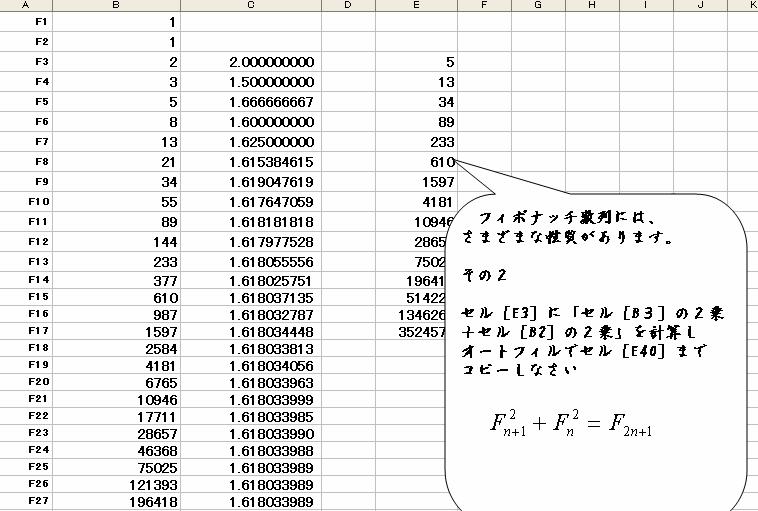
性質その2・・隣り合う2つのフィボナッチ数について2乗の合計を求めてください。 現れる数値もフィボナッチ数列の数値となります。
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
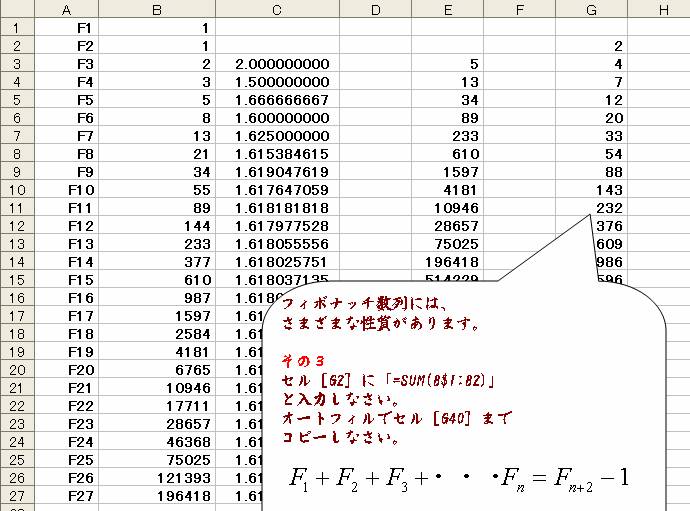
性質その3・F1からの累積は、フィボナッチ数列から1を引いた値となります。 ・ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
フィボナッチ数列には次のような公式もあります。 これを利用してフィボナッチ数の二乗のよる正方形を重ねて、螺旋形状を作成しましょう。
自然の中の渦巻きとフィボナッチ数とに何らかの関係があります。黄金比の関係で結びつきます。 次に黄金比の講座を参考ください。
|
フィボナッチ数列の勉強は以上です。お疲れ様でした。


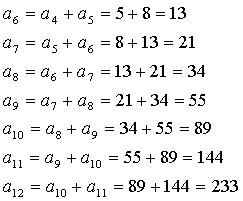
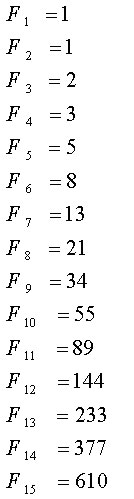
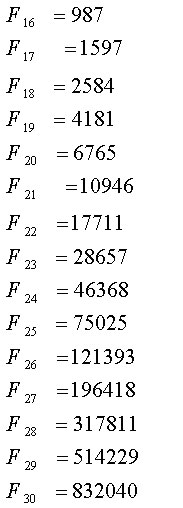
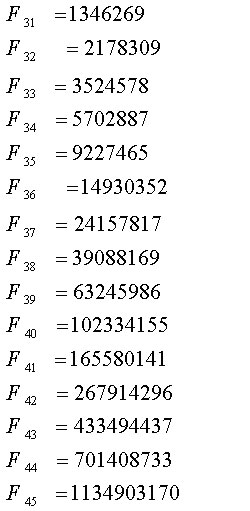
 2進数の増え方・・1,2,4,8、16,32・・・・・
2進数の増え方・・1,2,4,8、16,32・・・・・ フィボナッチ数列のような増え方1,1,2,3,5,8,13、21
フィボナッチ数列のような増え方1,1,2,3,5,8,13、21